2.1 三维空间刚体（Rigid Body）变换和相似（Similarity）变换 3D Rigid Body and Similarity Transformations

三维空间刚体变换 3D Rigid Body Transformations.

A 3D rigid body transform $\textbf{G} \in \text{SE(3)}$ denotes rotation and translation in 3D, i.e. is defined by

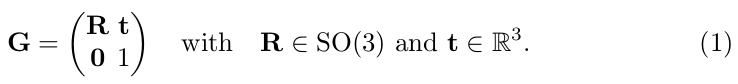
三维空间的刚体变换 (在欧氏空间求解，译者额外添加备注)（ $4\times4$ 矩阵） $\textbf{G} \in \text{SE(3)}$ ，定义了3D空间（位姿的）旋转和平移的转换关系，即公式（1）

During optimization, a minimal representation for the camera pose is required, which is given by the corresponding element $\mathbf{\xi} \in \mathfrak{se}(3)$ of the associated Lie-algebra.

在（通常的姿态图）优化过程中，相机位姿（最少）需要用到刚体变换 $\text{SE(3)}$ 李群对应的李代数 $\mathfrak{se}(3)$ 计算，即：（使用六维向量） $\mathbf{\xi} \in \mathfrak{se}(3)$ 。

Elements are mapped to $\text{SE(3)}$ by the exponential $\textbf{G} = \text{exp}_{\mathfrak{se}(3)}(\mathbf{\xi})$ , its inverse being denoted by $\mathbf{\xi} = \text{log}_{\text{SE(3)}}(\textbf{G})$ .

$\text{SE(3)}$ 和 $\mathfrak{se}(3)$ 的转换关系如下：使用指数映射关系（exponential map） $\textbf{G} = \text{exp}_{\mathfrak{se}(3)}(\mathbf{\xi})$ , 就可以把六维向量 $\mathbf{\xi}$ 从李代数 $\mathfrak{se}(3)$ 映射到刚体变换李群 $\text{SE(3)}$ 上（从而获得刚体变换矩阵 $\textbf{G}$ ），反之，使用对数映射关系 $\mathbf{\xi} = \text{log}_{\text{SE(3)}}(\textbf{G})$ ，就可以把 $\text{SE(3)}$ 上的刚体变换矩阵 $\textbf{G}$ 映射成在李代数 $\mathfrak{se}(3)$ 上的六维向量 $\mathbf{\xi}$ 。

With a slight abuse of notation, we consistently use elements of $\mathfrak{se}(3)$ to represent poses, which we directly write as vector $\mathbf{\xi} \in \mathbb{R}^6$ .

这里我们约定（当然不太严谨），使用 $\mathfrak{se}(3)$ 的六维向量 $\mathbf{\xi}$ （对时间算了微分才算是三个方向上的角速度和线速度组成前三个数表示平移 translation, 后三个数表示旋转 Rotation , 见参考书： Timothy D. Barfoot【STATE ESTIMATION FOR ROBOTICS】第217页）来表示位姿（变换），即： $\mathbf{\xi} \in \mathbb{R}^6$ 。

(公式摘录自Timothy D. Barfoot—STATE ESTIMATION FOR ROBOTICS 7.1.2小节Lie Algebras 第217页，译者额外添加备注)（感谢范帝楷的指点～～）

The transformation moving a point from frame $i$ to frame $j$ is written as $\mathbf{\xi}_{ji}$ .

一个（图像）点从图像帧 $i$ 到图像帧 $j$ 的变换，被记作： $\mathbf{\xi}_{ji}$ 。

For convenience, we define the pose concatenation operator $\circ : \mathfrak{se}(3) \times \mathfrak{se}(3) \rightarrow \mathfrak{se}(3)$

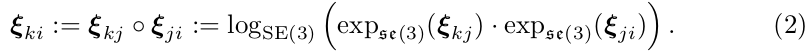
为了方便起见，我们定义位姿（变换）的结合律运算符，序连运算子（concatenation operator）◦ 即：se(3) × se(3) → se(3) ,见公式（2）

为了方便起见，我们在$\mathfrak{se}(3)$上定义一个乘法 $\circ$ （concatenation operator），即： $\circ : \mathfrak{se}(3) \times \mathfrak{se}(3) \rightarrow \mathfrak{se}(3)$ ，见公式（2）。

Further, we define the 3D projective warp function $\omega$ , which projects an image point $\textbf{p}$ and its inverse depth $d$ into a by $\mathbf{\xi}$ transformed camera frame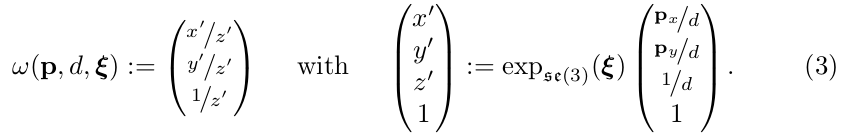

此外，我们还定义一个三维投影函数 $\omega$ （图像坐标到相机坐标系的投影函数），即：把图像上的某一点 $\textbf{p}$ 和这点的逆深度值 $d$ ，投影到由（ $\mathfrak{se}(3)$ 李代数下的六维向量） $\mathbf{\xi}$ 转换的相机坐标系下，公式（3）。

三维空间相似变换 3D Similarity Transformations.

A 3D similarity transform $\textbf{S} \in \text{Sim}(3)$ denotes rotation, scaling and translation, i.e. is defined by

三维空间（相似变换空间里，不是欧式空间，译者额外添加备注）的相似变换（ $4\times4$ ）矩阵 $\textbf{S} \in \text{Sim}(3)$ （相似变换空间）定义了旋转，尺度和平移的转换关系，即公式（4）。

As for rigid body transformations, a minimal representation is given by elements of the associated Lie-algebra $\mathbf{\xi} \in \mathfrak{sim}(3)$ , which now have an additional degree of freedom, that is $\mathbf{\xi} \in \mathbb{R}^7$ .

如同上述三维空间刚体变换，相似变换空间用对应的李代数 $\mathbf{\xi} \in \mathfrak{sim}(3)$ 表示，还要在向量 $\mathbf{\xi}$ 里额外加上一个自由度（即：尺度因子，译者额外添加备注），记作： $\mathbf{\xi} \in \mathbb{R}^7$ （七维向量，三个数表示旋转，三个数表示平移，一个数表示尺度因子，译者额外添加备注）。

The exponential and logarithmic map, pose concatenation and a projective warp function $\omega_{s}$ can be defined analogously to the $\mathfrak{se}(3)$ case, for further details see [23].

$\text{Sim(3)}$ 和 $\mathfrak{sim}(3)$ 之间的转换关系（即：指数映射和对数映射），位姿结合律运算符，序连运算子乘法（concatenation operator） $\circ : \mathfrak{sim}(3) \times \mathfrak{sim}(3) \rightarrow \mathfrak{sim}(3)$
和投影函数 $\omega_{s}$ ，与上述 $\mathfrak{se}(3)$ 的数学表达式相似，更多详情，请参考文献[23]。