3.5 （图优化）边（即：关键帧的约束关系）计算： $\mathfrak{sim}(3)$ 直接法配准 Constraint Acquisition: Direct $\mathfrak{sim}(3)$ Image Alignment

$\mathfrak{sim}(3)$ 直接法配准 Direct Image Alignment on $\mathfrak{sim}(3)$.

Monocular SLAM is – in contrast to RGB-D or Stereo-SLAM – inherently scale-ambivalent, i.e., the absolute scale of the world is not observable.

单目SLAM （系统）— 不同于RGB-D或双目SLAM — 具有尺度不确定性，（存在尺度漂移的问题，译者额外添加备注），即：场景的绝对尺度具有不可观性。

Over long trajectories this leads to scale-drift, which is one of the major sources of error [23].

所以，相机长距离的轨迹运动，会导致尺度漂移的问题，（即：尺度不确定性）是误差的主要产生原因之一，见论文[23]。

Further, all distances are only defined up to scale, which causes threshold-based outlier rejection or parametrized robust kernels (e.g. Huber) to be ill-defined.

此外，所有的距离（计算）都是取决于尺度，（如果尺度漂移，容易触发）外点（离群值，outlier）剔除或导致无法参数化核函数（比如：Huber核函数）。

We solve this by using the inherent correlation between scene depth and tracking accuracy:

我们通过利用场景深度（scene depth）和图像跟踪（配准）精度之间的内在相关性，来解决这个问题：

改动_Labby: 修改文字已插入原文

The depth map of each created keyframe is scaled such that the mean inverse depth is one.

每个关键帧的深度图被缩放至它的平均逆深度是1。

In return, edges between keyframes are estimated as elements of $\mathfrak{sim}(3)$ , elegantly incorporating the scaling difference between keyframes, and, in particular for large loop-closures, allowing an explicit detection of accumulated scale-drift.

这样，就可以使用相似变换 $\mathfrak{sim}(3)$ 来计算关键帧之间的边（即：约束关系），（因为）相似变换 $\mathfrak{sim}(3)$ 可以优雅较好地结合关键帧之间的尺度缩放差异，尤其是，针对大闭环（large loop-closures，产生的尺度漂移），很容易地（explicit）检测到累积的误差。

改动Labby: 优雅——>较好

（换句话说，见2.1小节，如果关键帧之间，使用刚体变换se(3)只有六个自由度，尺度不可控，会有尺度漂移的问题，所以换成使用sim(3)变换，因为多一个尺度因子作为第七个自由度，译者额外添加备注。）comment 思考不缜密

For this, we propose a novel method to perform $direct, scale-drift\ aware\ image\ alignment\ on\ \mathfrak{sim}(3)$ , which is used to align two differently scaled keyframes.

为此，我们设计一种新的算法，这个算法有如下特点：纠正尺度漂移，基于相似变换 $\mathfrak{sim}(3)$ ，直接法配准两帧（不同尺度缩放后的）关键帧。

In addition to the photometric residual $r_{p}$ , we incorporate a depth residual $r_{d}$ which penalizes deviations in inverse depth between keyframes, allowing to directly estimate the scaled transformation between them.

（为此，我们还修改误差函数 $E$ 的优化项）除了包含光度测量残差 $r_{p}$ （photometric residual，光度测量误差），我们还引入深度残差（depth residual） $r_{d}$ （充当惩罚变量项）来惩罚关键帧之间的逆深度偏差，（这个误差函数 $E$ 通过最小化优化，）能直接够估计出帧间的相似变换。

The total error function that is minimized becomes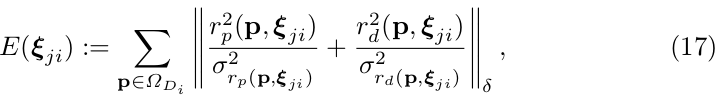

where the photometric residual $r_{p}^{2}$ and $\sigma_{r_{p}}^{2}$ is defined as in (13) - (14).

那么误差函数（error function 或叫做残差损失函数） $E$ 的最小化优化项，就改写成如下公式(17)，其中，光度测量残差 $r_{p}^{2}$ （photometric residual，光度测量误差项二次型）和它的方差 $\sigma_{r_{p}}^{2}$ 的数学定义，请见公式（13）—（14）。

The depth residual and its variance is computed as 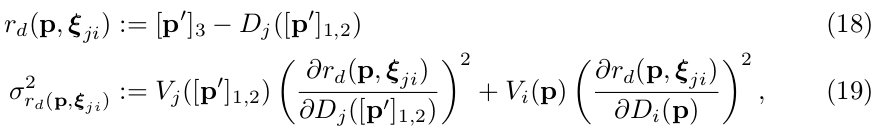where $\textbf{p}':=\omega_s(\textbf{p},D_{i}(\textbf{p}),\mathbf{\xi}_{ji})$ denotes the transformed point.

深度残差和它的方差计算分别如公式(18)和公式(19)，其中， $\omega_s$ 是相似变换投影函数， $\textbf{p}':=\omega_s(\textbf{p},D_{i}(\textbf{p}),\mathbf{\xi}_{ji})$ 是相似变换下转换到相机坐标系的点，（ $D_{j}(\begin{bmatrix}\textbf{p}'\end{bmatrix}_{1,2})$ 表示 $\textbf{p}'$ 对应关键帧 $j$ 的深度， $\begin{bmatrix}\textbf{p}'\end{bmatrix}_{3}$ 表示点 $\textbf{p}'$ 的深度，这里用到第二章开头的数学符号定义 $\begin{bmatrix}\cdot\end{bmatrix}_{n}$ ，译者添加额外备注，还需进一步理解，并对应代码）。

Note that the Huber norm is applied to the sum of the normalized photometric and depth residual – which accounts for the fact that if one is an outlier, the other typically is as well.

注意到，Huber范数作用在被归一化的光度测量残差（photometric residual）和深度残差（depth residual）之和上—如果两个残差中有一项不收敛，另外一项也不收敛。（此处需确认）

Note that for tracking on $\mathfrak{sim}(3)$ , the inclusion of the depth error is required as the photometric error alone does not constrain the scale.

还有，在 $\mathfrak{sim}(3)$ 上的图像跟踪，需要包括深度误差，因为仅有光度测量误差（photometric error）是不足以限定尺度（scale）。

Minimization is performed analogously to direct image alignment on $\mathfrak{se}(3)$ using the iteratively re-weighted Gauss-Newton algorithm (Sec. 2.2).

和 $\mathfrak{se}(3)$ 图像直接法类似， $\mathfrak{sim}(3)$ 的最小化（优化问题）是通过加权高斯—牛顿迭代算法实现的，请参考2.2小节。

In practice, $\mathfrak{sim}(3)$ tracking is computationally only marginally more expensive than tracking on $\mathfrak{se}(3)$, as only little additional computations are needed $^1$ .

虽然 $\mathfrak{sim}(3)$ 跟踪法比 $\mathfrak{se}(3)$ 跟踪法的计算成本要大，但是在实际（代码实现）中，只是略微增加小部分额外的计算量而已 $^1$ 。

$^1$ We approximate the gradient of the depth map to be zero, which significantly speeds up the computation.

$^1$ 我们把深度图的梯度近似为零，这样可以显著加快计算速度。image copy right belongs to engel14eccv paper， 图像摘录自 engel14eccv论文

Fig. 6: Two scenes with high scale variation. Camera frustums are displayed for each keyframe with their size corresponding to the keyframe’s scale.

示图6. 尺度变化比较大的两个场景。 （蓝色椎体代表相机视锥，或相机镜头）每一个关键帧上的相机视锥位姿在地图中被可视化（包括视锥尺寸大小和相应的关键帧尺度）。

约束条件检测（搜寻） Constraint Search.

After a new keyframe $\mathcal{K}_{i}$ is added to the map, a number of possible loop closure keyframes $\mathcal{K}_{j_{1}},...,\mathcal{K}_{j_{n}}$ is collected:

当新的一个帧关键帧 $\mathcal{K}_{i}$ 添加地图之后，进行闭环检测，即收集可能是（形成）闭环的（候选）关键帧 $\mathcal{K}_{j_{1}},...,\mathcal{K}_{j_{n}}$ 。

We use the closest ten keyframes, as well as a suitable candidate proposed by an appearance-based mapping algorithm [11] to detect large-scale loop closures.

为了检测大（尺度）闭环，我们使用最接近的十帧关键帧，以及由appearance-based mapping 算法[11] 筛选出来的候选帧。

To avoid insertion of false or falsely tracked loop closures, we then perform a reciprocal tracking check:

为了防止插入错误的或是假的闭环约束条件，我们要进行逆向相似度检测，即：

For each candidate $\mathcal{K}_{j_{k}}$ we independently track $\mathbf{\xi}_{j_{k}i}$ and $\mathbf{\xi}_{ij_{k}}$ .

对每一帧闭环候选帧 $\mathcal{K}_{j_{k}}$ ，我们独立去跟踪 $\mathbf{\xi}_{j_{k}i}$ 和 $\mathbf{\xi}_{ij_{k}}$ 。

Only if the two estimates are statistically similar, i.e., if

is sufficiently small, they are added to the global map.

当只有只有当这两个变换估计在统计上很相似，例如：（相似度检测）公式(20)的里面误差足够小的情况下(足够小的定义？译者额外添加备注)，这样的闭环约束（边）才被加入到全局地图里。

改动_Labby: 修改见文中

For this, the adjoint $\text{Adj}_{j_{k}i}$ is used to transform $\mathbf{\Sigma}_{ij_{k}}$ into the correct tangent space.

为此，我们引入一个伴随矩阵（或叫邻接矩阵） $\text{Adj}_{j_{k}i}$ ，作用就是把 $\mathbf{\Sigma}_{ij_{k}}$ 转换到正确的切线空间。（这里需代码确认）

Convergence Radius for $\mathfrak{sim}(3)$ Tracking.

$\mathfrak{sim}(3)$ 跟踪上的收敛半径 （按照Engel在Graz的报告，指图像帧和关键帧配准有关，来量化可以被跟踪的图像帧的多少，半径越大，说明可以被跟踪的图像帧越多，即和这帧关键帧做配准的图像帧越多，译者在其他论文, 比如说Automatic Evaluation of Landmarks for Image-Based Navigation Update，里面开头指出matching distance指的就是收敛半径，即，配准时预估位姿可能在的范围，需要代码确认，译者补充说明，需要确认）(这里所谓的收敛半径，是指优化目标函数时，初始值和真值之间的距离。如果直接法计算位姿时的初值离真值太远，有可能得到错误的结果)（谢谢贺一家点拨）

An important limitation of direct image alignment lies in the inherent non-convexity of the problem, and hence the need for a sufficiently accurate initialization.

用直接法来配准存在一个很大的局限性，就是非凸性，因此需要足够准确的初始位姿（initial guess） (这里可以参考清华大学高翔博士对直接法的介绍视频，译者额外添加备注，谢谢高翔博士的点拨)。

While for the tracking of new camera frames a sufficiently good initialization is available (given by the pose of the previous frame), this is not the case when finding loop closure constraints, in particular for large loop closures.

对于新图像帧的跟踪，可以由前一帧的相机姿态提供足够好的初始位姿，但是对于，找寻闭环约束条件，它的初始预估位姿往往不会很准确，尤其是对（长距离之后形成的）大闭环来说。

One solution for this consists in using a very small number of keypoints to compute a better initialization:

有一种解决思路就是使用少量的图像特征点，计算获取更好的初始位姿估计：

Using the depth values from the existing inverse depth maps, this requires aligning two sets of 3D points with known correspondences, which can be done efficiently in closed form using e.g. the method of Horn [13].

就是要配准两组已知对应关系的三维点云，其一，使用现有逆深度图的深度值，其二，使用（四元素）的封闭式解法，比如，Horn[13]提出的方法。

Still, we found that in practice the convergence radius is sufficiently large even for large-scale loop closures - in particular we found that the convergence radius can be substantially increased by the following measures:

然而，我们在实践中发现，即使对大闭环来说，收敛半径也是足够大 – 特别是我们发现，通过以下方法可以显着增加收敛半径（即：增大配准时预估位姿可能在的范围）：

– Efficient Second Order Minimization (ESM) [3]:

（ESM是Efficient Second-order Minimization的缩写，源自Benhimane和Malis在2004年在IROS上发表的工作。该算法采用重构误差平方作为衡量R和T相似性的指标，然后对于姿态空间进行了在李群（Lie Group）上的重新构建使得搜索的步长更为理性，在寻优上面使用的二阶近似的快速算法，译者网上资料搜寻，添加补充备注）

While our results confirm previous work [17] in that ESM does not significantly increase the precision of dense image alignment, we observed that it does slightly increase the convergence radius.

我们在[17]的工作中得到的（实验）结果论证，ESM在稠密（点云）图像配准的精度上不会有明显增加， 但是会稍微增大一点收敛半径（convergence radius）。

– Coarse-to-Fine Approach:

—由粗（配准）到细精（配准）的方法：

While a pyramid approach is commonly used for direct image alignment, we found that starting at a very low resolution of only 20 × 15 pixels – much smaller than usually done – already helps to increase the convergence radius.

直接法配准中经常使用到金字塔方法，（通过实验）我们发现，从非常低的分辨率开始，只有20x15（像素）——远远小于通常做的（分辨率设置）——就已经有效提高收敛半径。

An evaluation of the effect of these measures is given in Sec. 4.3.

这些方法的评估实验报告，请详见4.3小节。