3.3 对新图像帧的跟踪： $\mathfrak{se}(3)$ 直接图像配准 基于 $\mathfrak{se}(3)$ 的直接法配准 Tracking new Frames: Direct $\mathfrak{se}(3)$ Image Alignment

图示说明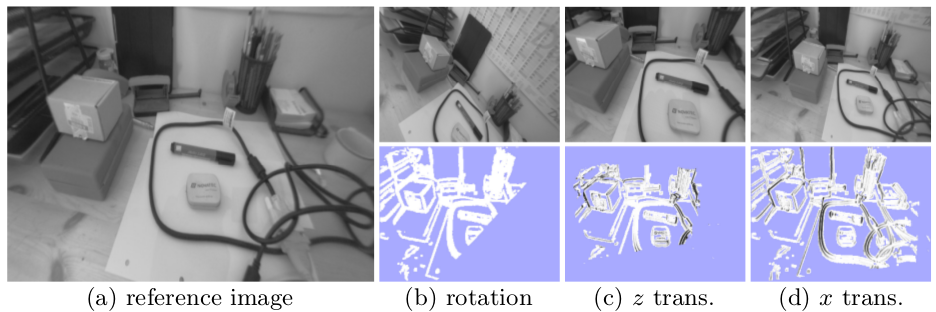： image copy right belongs to engel14eccv paper， 图像摘录自 engel14eccv论文

Fig. 4: Statistic normalization:

图示4：（残差方差的）统计归一化可视图示: （a） (把关键帧作为)图像参考帧 （b）相机旋转 （c）相机沿z轴平移 （d）相机沿x轴平移

解释：Patrick To Labby: 这里(a)最好翻译成参考帧，这里的参考帧是关键帧，可以参考LSD流程大框图。

(a) reference image. (b-d): tracked images and inverse variance $\sigma_{r_{p}}^{-2}$ of the residual.

（a）图像参考帧，（b-d）被跟踪的图像帧和残差的逆方差 $\sigma_{r_{p}}^{-2}$ 可视化示图。

For pure rotation, depth noise has no effect on the residual noise and hence all normalization factors are the same.

如果只有相机旋转（无平移），深度噪声对残差没有影响，因此所有归一化因子（normalization factor）都是相同的。

改动_Labby: 如果只有相机旋转（无平移）——>对于相机纯旋转运动

For $z$ translation depth noise has no effect for pixels in the center of the image, while for $x$ translation it only affects residuals with intensity-gradient in $x$ direction.

对于 $z$ 轴的相机平移，深度噪声对图像帧靠中间的像素区域没有影响，对于 $x$ 轴的相机平移，仅影响 $x$ 轴方向上强度梯度（比较显著）的残差。

改动_Labby: 对于 $z$ 轴的相机平移——>对于相机的轴向平移

Starting from an existing keyframe $\mathcal{K}_{i} = (I_{i},D_{i},V_{i})$ , the relative 3D pose $\mathbf{\xi}_{ji} \in \mathfrak{se}(3)$ of a new image $I_{j}$ is computed by minimizing the variance-normalized photometric error

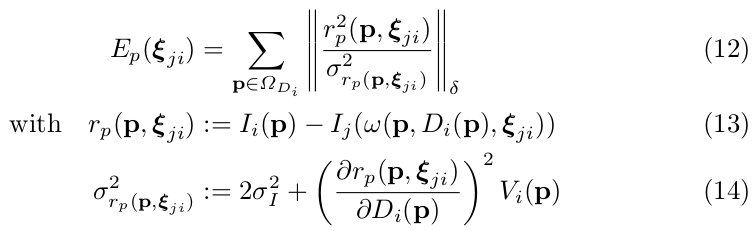
以当前关键帧 $\mathcal{K}_{i} = (I_{i},D_{i},V_{i})$ 作为参考帧，优化由方差归一化之后的光度误差项组成的最小二乘问题（见如下公式12,13,14），计算得到从关键帧 $\mathcal{K}_{i}$ 到新图象帧 $I_{j}$ 的相对（relative）三维空间姿态变换 $\mathbf{\xi}_{ji} \in \mathfrak{se}(3)$ 。

改动_Labby: 以当前关键帧作为参考帧，通过最小化方差归一化光度误差来计算当前帧图像相对参考帧的三维姿态变换。

where $\|\cdot\|_{\delta}$ is the Huber norm applied to the $normalized$ residual.

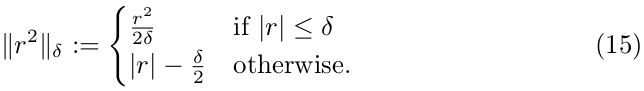
其中， $\|\cdot\|_{\delta}$ 是Huber范数，（见公式15），应用于归一化的残差上。

The residual’s variance $\sigma_{r_{p}(\textbf{p},\mathbf{\xi}_{ji})}^{2}$ is computed using covariance propagation as described in Sec. 2.3, and utilizing the inverse depth variance $V_{i}$ .

通过计算协方差传递公式得到残差方差 $\sigma_{r_{p}(\textbf{p},\mathbf{\xi}_{ji})}^{2}$ ，原理简述在2.3小节，这里使用了逆深度方差 $V_{i}$ 。

Further, we assume Gaussian image intensity noise $\sigma_{I}^2$ .

此外，我们假设高斯图像强度（像素灰度）噪声是 $\sigma_{I}^2$ 。

改动_Labby: 此外，我们假设图像灰度噪声服从高斯分布。

Minimization is performed using iteratively re-weighted Gauss-Newton optimization as described in Sec. 2.2.

通过加权高斯-牛顿迭代优化这个最小二乘的最小化问题，请参考2.2小节。

改动_Labby: 通过迭代重加权高斯-牛顿优化方法使目标函数最小化，请参考2.2小节。

In contrast to previous direct methods, the proposed formulation explicitly takes into account varying noise on the depth estimates:

我们提出的公式与之前的直接法不同，即公式明确地考虑了深度估计中各种（不同相机运动产生的）噪声和之前直接法不同的是，我们将深度噪声引入到了最小化光度误差的公式中：（谢谢贺一家点拨）

This is of particular relevance as for direct, monocular SLAM, this noise differs significantly for different pixels, depending on how long they were visible – which is in contrast to approaches working on RGB-D data, for which the uncertainty on the inverse depth is approximately constant.

对于直接 法的单目SLAM系统来说，不同像素的深度噪声是不同的，完全取决于这个像素被观测到多少次。不确定性表现为，像素不同，深度噪声也不同，这取决于像素在时间上的可观性（visible）—它与RGB-D数据的工作方式不同，即：后者逆深度的不确定性是近似常数。（谢谢贺一家点拨）

Figure 4 shows how this weighting behaves for different types of motion.

参见示图4. 不同类型的相机运动，深度噪声（即深度不确定性）如何作用在图像像素上（进行加权）的。

Note that no depth information for the new camera image is available – therefore, the scale of the new image is not defined, and the minimization is performed on $\mathfrak{se}(3)$ .

注意到的是，假设新图像帧的深度信息不可用，就不会定义新图像帧的尺度，然后就在 $\mathfrak{se}(3)$ 上进行最小化优化。